Ancillary Results About Polynomials
Definition 1
Let 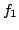 and
and 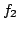 be polynomials. If
be polynomials. If 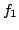 and
and 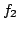 have no non-trivial common factor, then they are said to be
coprime. That is,
have no non-trivial common factor, then they are said to be
coprime. That is, 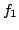 and
and 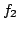 are
coprime if
are
coprime if 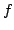 is a constant polynomial whenever
is a constant polynomial whenever 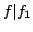 and
and 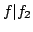 .
.
Theorem 1 (Euclid's algorithm)
Let 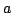 ,
, 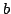 be polynomials. Then there exist polynomials
be polynomials. Then there exist polynomials 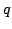 ,
, 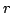 with
with 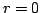 or
or
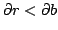 such that
such that
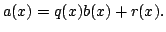
Euclid's algorithm is really just long division. We are applying it
here to polynomials, where ![]() is the `quotient' and
is the `quotient' and ![]() is the
`remainder'.
is the
`remainder'.
This is a corollary of Euclid's algorithm, and is equivalent to the definition of coprimality.
Gihan Marasingha 2005-09-19